Distributions

Table of Contents

I. Hypergeometric distribution

Physical setup

Suppose we have a collection of $N$ objects which can be classified into two distinct categories. Denote the categories:

Success ( $S$ )
Failure ( $F$ )

Suppose that within these $N$ objects there exist $r$ of type $S$ and therefore $N-r$ of type $F$ . We choose $n$ objects without replacement, that is, we remove items in succession from the original set of $N$ . Let $X$ be a random variable representing the number of successes obtained. Then $X$ has a hypergeometric distribution.

Probability function

We require three values. Refer to the primer on combinations for a discussion on counting rules and notation.

First, we require the total possible number of ways that $n$ distinct items can be chosen from $N$ without replacement and where order does not matter. This is ‘ $N$ Choose $n$ ’

$\binom{N}{n}$

Second, we wish to know the number of ways that $x$ successes can be drawn from a total of $r$

$\binom{r}{x}$

Third, we are left to select $n-x$ failures from a total of $N-r$

$\binom{N-r}{n-x}$

Then the probability of selecting $x$ successes is

$f(x; N,n,r) = \frac{\binom{r}{x}\cdot\binom{N-r}{n-x}}{\binom{N}{n}} \text{ for }x=0,1,\cdots,r$

Examples

A Deck of cards

A deck of playing cards contains 4 suits (hearts, spade, diamonds,clubs) for each of 13 types {Ace, 2, 3,…, 10, King, Queen, Jack}. Deal 5 cards from the deck. The probability of selecting up to four Aces from the deck follows a hypergeometric distribution

$f(x) = \frac{\binom{4}{x}\cdot\binom{52-4}{5-x}}{\binom{52}{5}}$

# Probability of selecting Aces from a standard deck of cards

# Initialize our relevant variables
nAces <- 4 # Available aces
nOther <- 48 # Available non-aces
nDeal  <- 5 # Number of cards dealt
aces <- 0:4 # The vector declaring the number of aces

# Use the dhyper built-in function for hypergeometric probability
probability <- dhyper(aces, nAces, nOther, nDeal, log = FALSE)
data <- data.frame( x = aces, y = probability )

# Bar plot
library(ggplot2)
ggplot(data, aes(x=factor(x), y=y)) +
  theme(axis.text=element_text(size=14),
        axis.title=element_text(size=18,face="bold"),
        axis.title.x=element_text(margin=margin(20,0,0,0)),
        axis.title.y=element_text(margin=margin(0,20,0,0))
        ) +
  geom_bar(stat="identity", fill= "#2c3e50", colour="black") +
  labs(x = "Number of Aces", y = "Probability")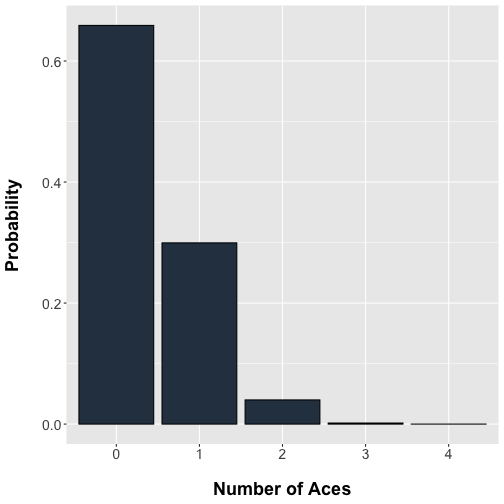

plot of chunk unnamed-chunk-1

II. Binomial distribution

Physical setup

Consider an experiment in which we have two distinct types of outcomes that can be categorized as

Success ( $S$ )
Failure ( $F$ )

Suppose the probability of success is $p$ and failure is $(1-p)$ . Repeat the experiment $n$ independent times. If $X$ is the number of successes then it has a binomal distribution denoted $X\sim Bi(n, p)$ .

Probability function

We require three values. Refer to the primer on combinations for a discussion on counting rules and notation.

First, we require the total possible number of ways that $x$ successes can be arranged within $n$ experiments which is

$\begin{equation*} \begin{split} \frac{n!}{x!(n-x!)} &= \binom{n}{x} \end{split} \end{equation*}$

Then the probability of each arrangement is $p$ multiplied $x$ times for successes and likewise for failures

$\begin{equation*} \begin{split} p^x(1-p)^{n-x} \end{split} \end{equation*}$

Therefore,

$\begin{equation*} \begin{split} f(x; n,p) &= \binom{n}{x} p^x(1-p)^{n-x} \text{ for }x=0,1,\cdots,n\\ \end{split} \end{equation*}$

Moments

The mean of a binomial distribution of sample size $n$ and probability $p$ is

$\begin{equation*} E[X] = np \end{equation*}$

The variance is

$\begin{equation*} Var(X) = np(1-p) \end{equation*}$

Comparison of hypergeometric and binomial

The key difference between the hypergeometric and the binomial distribution is that the hypergeometric involves the probability of an event when selection is made without replacement. In other words, the hypergeometric setup assumes some dependence amongst the selection of successes and failures. For example, choosing an ace from a deck and removing it reduces the probability of selecting a remaining ace. In contrast, the binomial distribution assumes independence and can be viewed as appropriate when event selection is made with replacement.

There are limiting cases where the hypergeometric can be approximated by the binomial. Consider the hypergeometric case where the total number of possible successes and failures $N$ is large compared to the number of selections $n$ . Then the probability of success $p=r/N$ does not appreciably upon selection without replacement. That is, for $N>>n$

$\begin{equation*} \begin{split} \frac{\binom{r}{x}\cdot\binom{N-r}{n-x}}{\binom{N}{n}} &\approx \binom{n}{x} \left(\frac{r}{N}\right)^x \left(1 - \frac{r}{N}\right)^{(n-x)} \end{split} \end{equation*}$

Examples

A fair die

Toss a fair die 10 times and let $X$ be the number of sixes then $X\sim Bi(10,1/6)$ .

$f(x) = \binom{10}{x} (1/6)^x(1-(1/6))^{10-x}$

# Probability of sixes in 10 tosses of a fair die
# Initialize our relevant variables
trials <- 10
sixes  <- 0:10 # The vector declaring the number of successes
p      <- 1/6  # The probability of a given face

# Use the dbinom built-in function for binomial probability
probability <- dbinom(sixes, size=trials, prob=p)
data <- data.frame( x = sixes, y = probability )

# Bar plot
library(ggplot2)
ggplot(data, aes(x=factor(x), y=y)) +
  theme(axis.text=element_text(size=14),
        axis.title=element_text(size=18,face="bold"),
        axis.title.x=element_text(margin=margin(20,0,0,0)),
        axis.title.y=element_text(margin=margin(0,20,0,0))
        ) +
  geom_bar(stat="identity", fill= "#2c3e50", colour="black") +
  labs(x = "Number of Sixes", y = "Probability")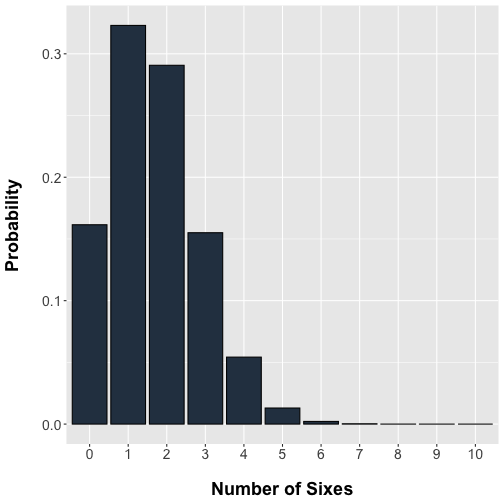

plot of chunk unnamed-chunk-2

III. Poisson distribution

Physical setup

Consider a limiting case of the binomial distribution as $n\rightarrow\infty$ and $p\rightarrow 0$ but $np=\mu$ is fixed. This means that the event of interest is relatively rare. Then $X$ has a Poisson distribution $P \sim Poisson(\mu)$ .

Probability function

Since $np=\mu$ then $p=\frac{\mu}{n}$ and

$\begin{equation*} \begin{split} f(x; n,p) &= \binom{n}{x} p^x(1-p)^{n-x} \\ f(x; n,\mu) &= \frac{n!}{x!(n-x)!} \left(\frac{\mu}{n}\right)^x \left(1-\frac{\mu}{n}\right)^{(n-x)} \\ &= \frac{\mu^x}{x!} \frac{n(n-1)(n-2)\cdots(n-x+1)}{(n)(n)(n)\cdots(n)} \left(1-\frac{\mu}{n}\right)^{(n-x)} \\ &= \frac{\mu^x}{x!} \left(\frac{n}{n}\right) \left(\frac{n-1}{n}\right) \left(\frac{n-2}{n}\right) \cdots \left(\frac{n-x+1}{n}\right) \left(1-\frac{\mu}{n}\right)^n \left(1-\frac{\mu}{n}\right)^{-x}\\ \lim_{n\to\infty} f(x; n,\mu) &= \frac{\mu^x}{x!} (1)(1)(1) \cdots (1) e^{-\mu} (1)^{-x}\\ f(x; \mu) &= \frac{\mu^x}{x!}e^{-\mu} \text{ for }x=1,2,\cdots\\ \end{split} \end{equation*}$

Moments

The mean of a Poisson distribution with some sampling size $n$ and probability $p$ is

$\begin{equation*} E[X] = np \end{equation*}$

The variance is

$\begin{equation*} Var(X) = E[X] \end{equation*}$

Examples

The birthday game

Suppose that 200 people are at a party. What is the probability that 2 of them were born on December 25th? In this case $n=200$ and assuming birthdays are independent then $p=1/365$ and the mean $\mu=np$

$f(x) = \frac{ \left(\frac{200}{365}\right)^x}{x!} e^{-\left(\frac{200}{365}\right)}$

# Probability of two people born on December 25th
# Initialize our relevant variables
n  <- 200   # The number of people
p  <- 1/365 # The probability of a birthday on Dec. 25
mu <- n*p   # The mean

# Use the dpois built-in function for Poisson probability
probability <- dpois(2, mu, log = FALSE)
probability

## [1] 0.086791

IV. Gamma distribution

Gamma function

Definition The gamma function os $\alpha$ is

$\begin{equation*} \Gamma(\alpha) = \int_{0}^{\infty} x^{\alpha-1}e^{-x}dx \end{equation*}$

There are two nice properties of the gamma function that we will use.

$\Gamma(\alpha) = (\alpha - 1)\Gamma(\alpha - 1) \text{ for } \alpha>1$
$\Gamma(\alpha) = (\alpha - 1)! \text{ if } \alpha \text{ is a positive integer}$

Gamma distribution

Let $X$ be a non-negative continuous random variable. Then if the probability function is of the form

$\begin{equation*} f(x; \alpha, \beta) = \frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x} \end{equation*}$

then $X$ has a gamma distribution $X\sim Gamma(x; \alpha,\beta)$ . Typically, $\alpha$ is called the ‘shape’ parameter and $\beta$ the ‘scale’ or ‘rate’.

V. Negative binomial distribution

Physical setup

The setup is very similar to the binomial. Consider an experiment in which we have two distinct types of outcomes that can be categorized as

Success ( $S$ )
Failure ( $F$ )

Suppose the probability of success is $p$ and failure is $(1-p)$ . Repeat an experiment until a pre-specified number of failures $r$ have been obtained. Let $X$ be the number of successes before the $r^{th}$ failure. Then $X$ has a negative binomial distribution denoted $X\sim NB(r, p)$ .

Probability function

There will be $x+r$ total trials but the last event is a failure so we really care about the first $x+r-1$ trials. There will be $x$ successes and $(r-1)$ failures in any order. Each order has a probability identical to a binomial trial $p^x(1-p)^r$ .

$\begin{equation*} \begin{split} f(x; r,p) &= \binom{x+r-1}{x} p^x(1-p)^r \text{ for }x=0,1,2,\cdots\\ \end{split} \end{equation*}$

Moments

The mean of a negative binomial distribution is

$\begin{equation*} E[X] = \frac{pr}{1-p} \end{equation*}$

The variance is

$\begin{equation*} Var(X) = \frac{pr}{(1-p)^2} \end{equation*}$

The Poisson-gamma mixture

Count data such as RNA sequencing mapped reads is often modeled with a Poisson distribution where the mean and variance are equal to $\mu$ . However, there are cases where the variance exceeds that specified by the mean. To account for this ‘overdispersed’ data, the negative binomial distribution can be utilized. As we will show below, the negative binomial arises as a Poisson distribution where the Poisson parameter is itself a random variable distributed according to a Gamma distribution.

Let us state this in a more precise fashion. Suppose that we have distribution of counts $X$ that follows a Poisson distribution indexed by the parameter $\Theta$ . Now suppose that $\Theta$ is itself some function of another random variable $\Theta = \mu\epsilon$ where $\epsilon \sim Gamma(x;\alpha,\beta)$ . Then the conditional distribution of the random variable of counts is

$\begin{equation*} P(X=x | \Theta = \mu\epsilon) = \frac{(\mu\epsilon)^x}{x!}e^{- (\mu\epsilon)} \text{ for } x=0,1,2,\cdots \end{equation*}$

Let $\epsilon$ follow a gamma distribution with shape $\alpha$ and scale $\beta$ .

$\begin{equation*} g(\epsilon) = \frac{\beta^\alpha}{\Gamma(\alpha)}\epsilon^{\alpha-1}e^{-\beta \epsilon} \end{equation*}$

The joint density of $N$ and $\Theta$ is

$\begin{equation*} \begin{split} P(X=x | \Theta = \mu\epsilon) \cdot g(\epsilon) &= \frac{(\mu\epsilon)^x}{x!}e^{- \mu\epsilon} \cdot \frac{\beta^\alpha}{\Gamma(\alpha)}\epsilon^{\alpha-1}e^{-\beta \epsilon}\\ \end{split} \end{equation*}$

Derive the marginal distribution of $X$ by integrating over the values of $epsilon$ .

$\begin{equation*} \begin{split} P(X=x) &= \int_{0}^\infty \frac{(\mu\epsilon)^x}{x!}e^{- \mu\epsilon} \cdot \frac{\beta^\alpha}{\Gamma(\alpha)}\epsilon^{\alpha-1}e^{-\beta \epsilon} d\epsilon\\ &= \frac{\mu^x\beta^\alpha}{x! \Gamma(\alpha)} \int_{0}^\infty \epsilon^{x+\alpha-1} e^{-(\beta + \mu)\epsilon} d\epsilon\\ \end{split} \end{equation*}$

The key here is to transform the integrand into a gamma distribution with shape parameter $x+\alpha$ and scale $\beta+\mu$ and noting that the integral over all values is unity.

$\begin{equation*} \begin{split} P(X=x) &= \frac{\mu^x \beta^\alpha}{x! \Gamma(\alpha)} \frac{\Gamma(x+\alpha)}{(\beta + \mu)^{x + \alpha}} \int_{0}^\infty \frac{(\beta + \mu)^{x + \alpha}}{\Gamma(x+\alpha)} \epsilon^{x+\alpha-1} e^{-(\beta + \mu)\epsilon} d\epsilon \\ &= \frac{\Gamma(x+\alpha)}{x! \Gamma(\alpha)} \frac{\mu^x \beta^\alpha}{(\beta + \mu)^{x + \alpha}} \\ &= \frac{(x+\alpha-1)!}{x! (\alpha - 1)!} \frac{\mu^x}{(\beta + \mu)^x} \frac{\beta^\alpha}{(\beta + \mu)^{\alpha}} \\ &= \binom{x+\alpha-1}{x} \left(\frac{\mu}{\beta + \mu }\right)^x \left(\frac{\beta}{\beta + \mu}\right)^\alpha \text{ for }x=0,1,\cdots \end{split} \end{equation*}$

It is simple to see that this result is the negative binomial with $r=\alpha$ and $p=\mu/(\beta+\mu)$ . In this case the moments can be stated using these new variables.

From the moments of the negative binomial stated above, the mean is

$\begin{equation*} \begin{split} E[X] &= \left(\frac{\mu}{\beta + \mu}\right) \left(\frac{\beta + \mu}{\beta}\right) \alpha\\ &= \frac{\alpha}{\beta} \mu\\ \end{split} \end{equation*}$

The variance is

$\begin{equation*} \begin{split} Var(X) &= \left(\frac{\mu}{\beta + \mu}\right) \left(\frac{\beta + \mu}{\beta}\right)^2 \alpha\\ &= \frac{\alpha \mu}{\beta} \left(1 + \frac{\mu}{\beta} \right)\\ \end{split} \end{equation*}$

Alternative Poisson-gamma notation

This mixture model will be important in our discussion of RNA sequencing data differential expression testing. In this case the notation is altered where $r=\alpha=\beta=\phi^{-1}$ and $\phi$ is the ‘dispersion’ parameter for some counts of an RNA species $Y$ . Also the gamma function is used to replace the binomial coefficients.

$\begin{equation*} \begin{split} Y &\sim NB(\mu, \phi^{-1})\\ f(y; \mu,\phi^{-1}) &= \frac{\Gamma(y+\phi^{-1})}{\Gamma(y+1)\Gamma(\phi^{-1})} \left(\frac{\mu}{\phi^{-1} + \mu} \right)^y \left(\frac{\phi^{-1}}{\phi^{-1} + \mu} \right)^{\phi^{-1}} \\ \end{split} \end{equation*}$

From the above discussion, we can restate the mean and variance.

$\begin{equation*} \begin{split} E[Y] &= \mu\\ Var(Y) &= \mu + \phi\mu^2\\ \end{split} \end{equation*}$

Note that as the dispersion parameter $\phi$ approaches zero the negative binomial variance approaches the mean. Thus the dispersion parameter accounts for the extra variability over and above that expected with a Poisson.

Pathway Guide

Distributions

I. Hypergeometric distribution

Physical setup

Probability function

Examples

A Deck of cards

II. Binomial distribution

Physical setup

Probability function

Moments

Comparison of hypergeometric and binomial

Examples

A fair die

III. Poisson distribution

Physical setup

Probability function

Moments

Examples

The birthday game

IV. Gamma distribution

Gamma function

Gamma distribution

V. Negative binomial distribution

Physical setup

Probability function

Moments

The Poisson-gamma mixture

Alternative Poisson-gamma notation