Permutations & Combinations

---

Permutations

Suppose that $n$ distinct objects are drawn sequentially, ordered from left to right in row. Keep in mind that order matters and that objects are drawn without replacement, that is, the pool of objects to be drawn from decreases with each selection.

1. The number of ways to arrange $n$ distinct objects in a row is

   $$n(n-1)(n-2)\dotsm(2)(1)=n!$$

   where the $!$ symbol is described as “factorial”.

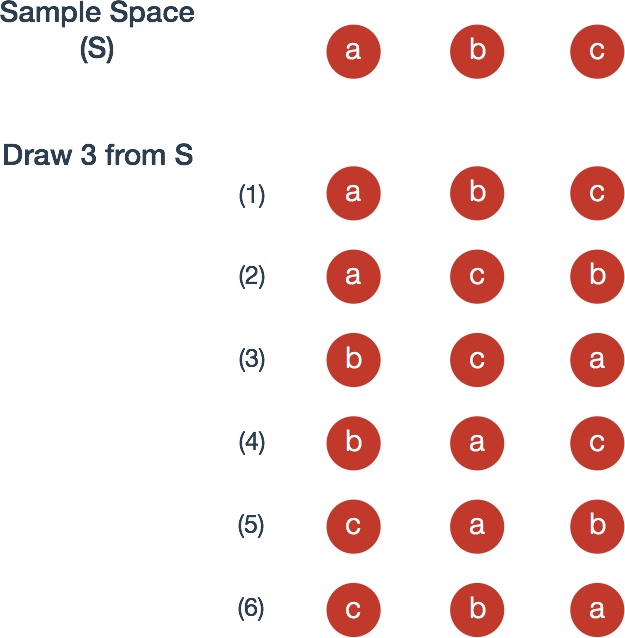
   For example, consider three numbered balls; They can be arranged $3!= (3)(2) = 6$ different ways.

   

2. The number of ways to arrange $r$ objects selected from $n$ distinct objects is

   $$n(n-1)(n-2)\dotsm(n-r+1)=n^{(r)}$$

   where the $n^{(r)}$ notation describes “n taken to r terms”. An alternative expression for this is

   $$n^{(r)}=n(n-1)\dotsm(n-r+1)[\frac{(n-r)(n-r-1)\dotsm(2)(1)}{(n-r)(n-r-1)\dotsm(2)(1)}]=\frac{n!}{(n-r!)}$$

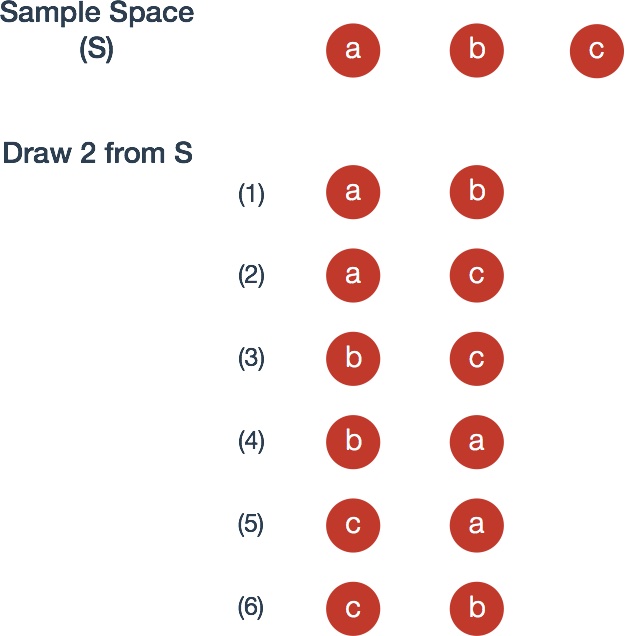
   For example, consider again three numbered balls; Two balls can be arranged $\frac{3!}{(3-2)!}=6$ different ways.

---

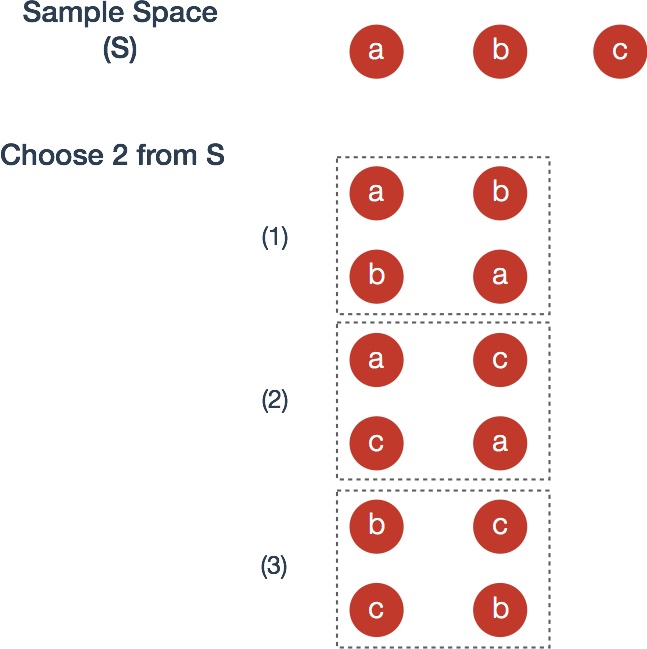
Combinations

Suppose that order does not matter and as before, objects are drawn without replacement.

Now, the number of ways to choose $r$ objects from n distinct objects is

$$\binom{n}{r}=\frac{n!}{r!(n-r)!}=\frac{n(n-1)\dotsm(n-r+1)(n-r)(n-r-1)\dotsm(2)(1)}{r!(n-r)(n-r-1)\dotsm(2)(1)}=\frac{n^{(r)}}{r!}$$

where the $\binom{n}{r}$ symbol is “n choose r”.

Proof From permutations rule 2, recall that the ways we can arrange $r$ objects from $n$ objects is $n^{(r)}$. Any choice of $r$ objects can be ordered $r!$ different ways. It follows that

$$(\text{number of ways to choose r from n})\cdot r!=n^{(r)}$$

Concretely, the image below is nearly identical to the example for permutations rule 2 except that, since order is ignored, we group those with identical elements with a dotted box, leaving three events rather than the previous six